Tags
- Queue
- 스택
- DB
- Article & User
- 큐
- migrations
- outer join
- Vue
- distinct
- SQL
- Django
- 그리디
- update
- 통계학
- M:N
- stack
- drf
- ORM
- 트리
- create
- Tree
- delete
- regexp
- 쟝고
- 뷰
- 이진트리
- 백트래킹
- 완전검색
- N:1
- count
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
스택 - Memoization 본문
1. 재귀호출의 문제점
이전의 설명한 재귀호출 (2024.05.26 - [백엔드] - 재귀호출)의 문제점은 엄청난 중복 호출이 존재합니다.
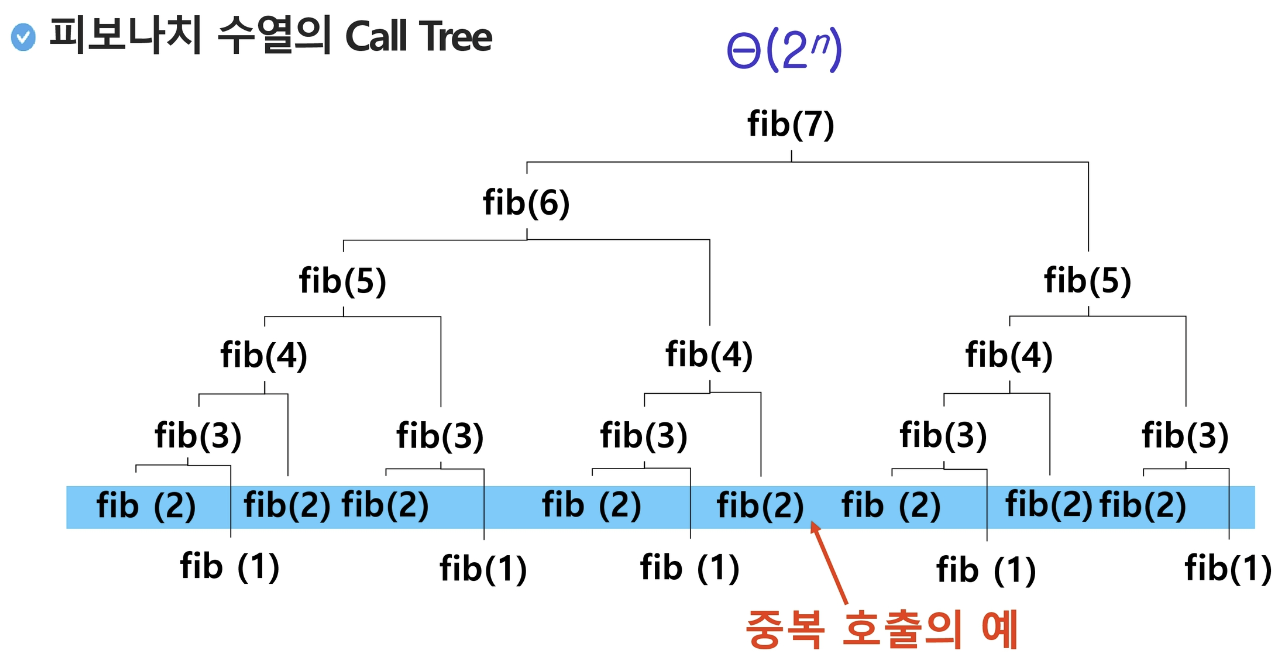
2. Memoization
- 메모이제이션(memoization)은 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술입니다. 동적 계획법의 핵심이 되는 기술입니다.
- 'memoization'은 글자 그대로 해석하면 '메모리에 넣기(to put in memory)'라는 의미이며 ' 기억되어야 할 것'이라는 뜻의 라틴어 memorandum에서 파생되었다. 흔히 '기억하기', '암기하기'라는 뜻의 memorization과 혼동하지만, 정확한 단어는 memoization이다. 동사형은 memoize이다.
- 앞의 예시에서 피보나치 수를 구하는 알고리즘에서 fibo(n)의 값을 계산하자마자 저장하면(memoize), 실행시간을 Θ(n)으로 줄일 수 있다.
- Memoization 방법을 적용한 알고리즘은 다음과 같다.
# memo를 위한 배열을 할당하고, 모두 0으로 초기화 한다;
# memo[0]을 0으로 memo[1]는 1로 초기화 한다;
def fibo1(n):
global memo
if n>= 2 and memo[n] == 0:
memo[n] = (fibo1(n-1) + fibo1(n-2))
return memo[n]
memo = [0] * (n+1)
memo[0] = 0
memo[1] = 1'알고리즘' 카테고리의 다른 글
| 스택 - 계산기1 (0) | 2024.06.02 |
|---|---|
| 스택 - DFS(깊이우선탐색) (0) | 2024.06.01 |
| 스택 - DP(Dynamic Programming) (0) | 2024.05.31 |
| 스택 - 재귀호출 (0) | 2024.05.29 |
| 스택(stack) (0) | 2024.05.28 |





