Tags
- Vue
- delete
- migrations
- 스택
- SQL
- drf
- 그리디
- Tree
- 완전검색
- create
- M:N
- 통계학
- Queue
- 백트래킹
- ORM
- Article & User
- regexp
- update
- outer join
- distinct
- 쟝고
- Django
- N:1
- count
- DB
- 이진트리
- 뷰
- 트리
- 큐
- stack
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Notice
Recent Posts
Link
데이터 분석 기술 블로그
스택 - 백트래킹 본문
1. 백트래킹
- 백트래킹 (Backtracking) 기법은 해를 찾는 도중에 '막히면' (즉, 해가 아니면) 되돌아가서 다시 해를 찾아가는 기법입니다.
- 백트래킹 기법은 최적화 (optimization) 문제와 결정 (decision) 문제를 해결할 수 있습니다.
- 결정 문제 : 문제의 조건을 만족하는 해가 존재하는지의 여부를 'yes' 또는 'no'가 답하는 문제입니다.
- 미로 찾기
- n-Queen 문제
- Map coloring
- 부분 집합의 합(Subset Sum) 문제 등
- 백트래킹과 깊이 우선탐색과의 차이
- 어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄입니다. (Prunning 가지치기)
- 깊이우선탐색이 모든 경로를 추적하는데 비해 백트래킹은 불필요한 경로를 조기에 차단합니다.
- 깊이우선탐색을 가하기에는 경우의 수가 너무나 많습니다. 즉, N! 가지의 경우의 수를 가진 문제에 대해 깊이우선탐색을 가하면 당연히 처리 불가능한 문제입니다.
- 백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 이 역시 최악의 경우에는 여전히 지수함수 시간(Exponential Time)을 요하므로 처리 불가능합니다.
- 모든 후보를 검사?
- No!
- 백트래킹 기법
- 어떤 노드의 유망성을 점검한 후에 유망(promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(backtracking) 다음 자식 노드로 갑니다.
- 어떤 노드를 방문하였을 때 그 노드를 포함한 경로가 해답이 될 수 없으면 그 노드는 유망하지 않다고 하며, 반대로 해답의 가능성이 있으면 유망하다고 합니다.
- 가지치기(pruning) : 유망하지 않는 노드가 포함되는 경로는 더 이상 고려하지 않습니다.
- 백트래킹을 이용한 알고리즘은 다음과 같은 절차로 진행됩니다.
- 상태 공간 트리의 깊이 우선 검색을 실시합니다.
- 각 노드가 유망하지를 점검합니다.
- 만일 그 노드가 유망하지 않으면, 그 노드의 부모 노드로 돌아가서 검색을 계속합니다.



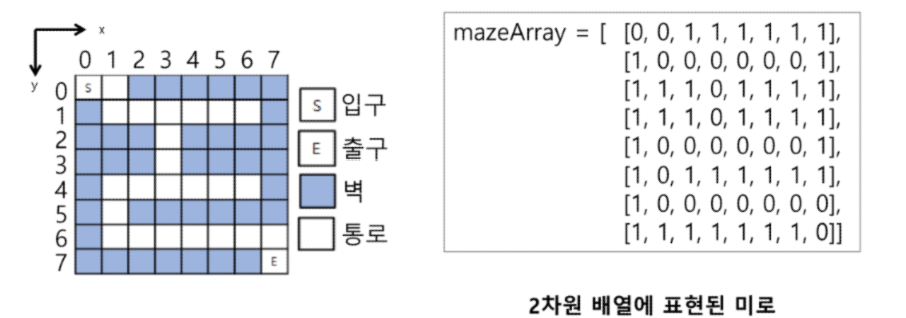
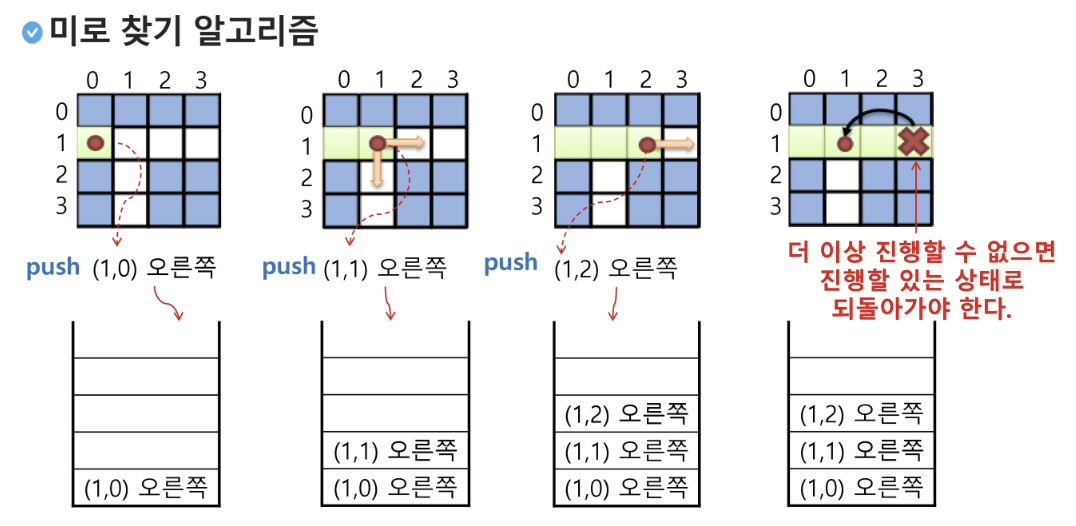
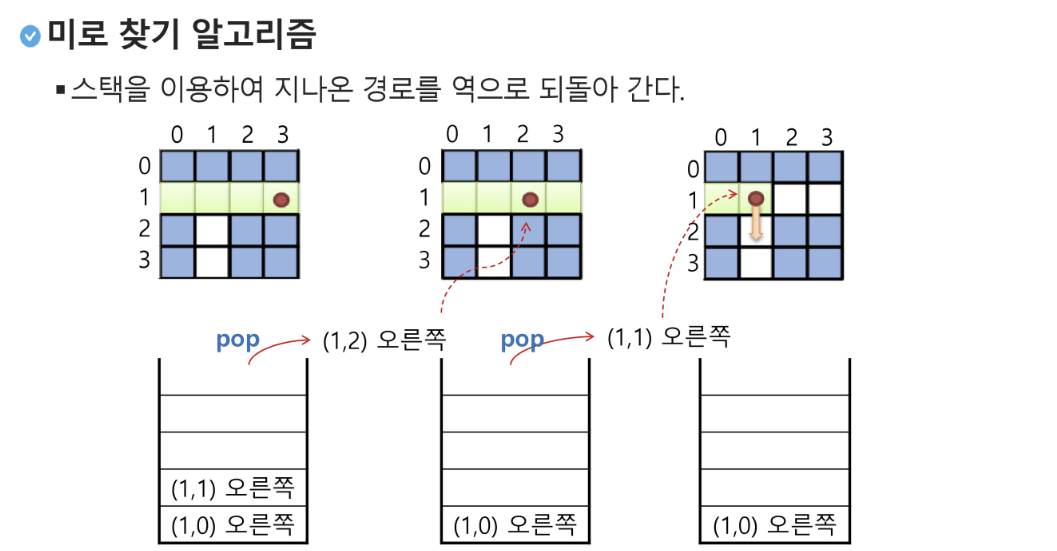
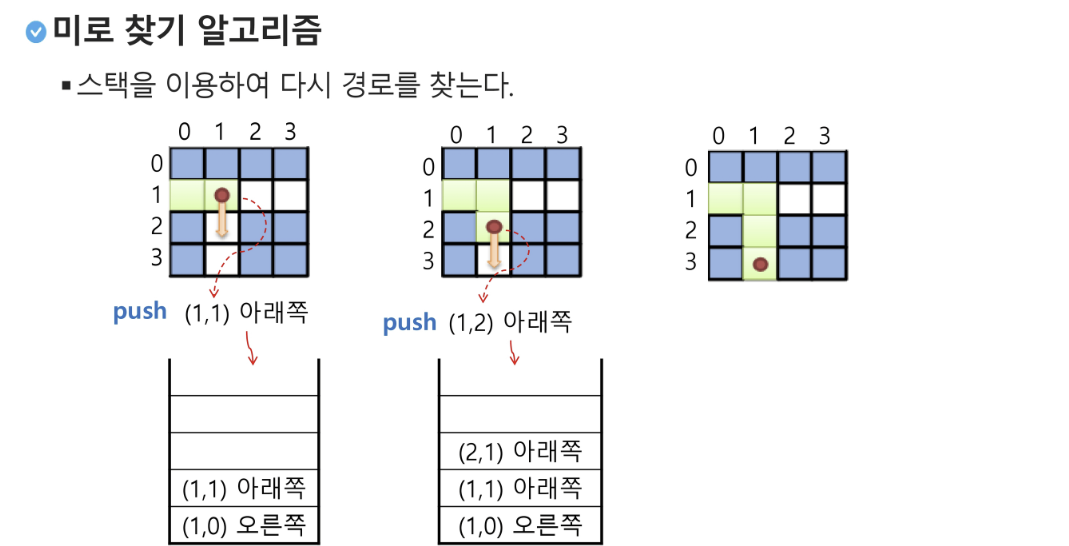
2. 미로 찾기
- 아래 그림과 같이 입구와 출구가 주어진 미로에서 입구부터 출구까지의 경로를 찾는 문제입니다.
- 이동할 수 있는 방향은 4방향으로 제한합니다.
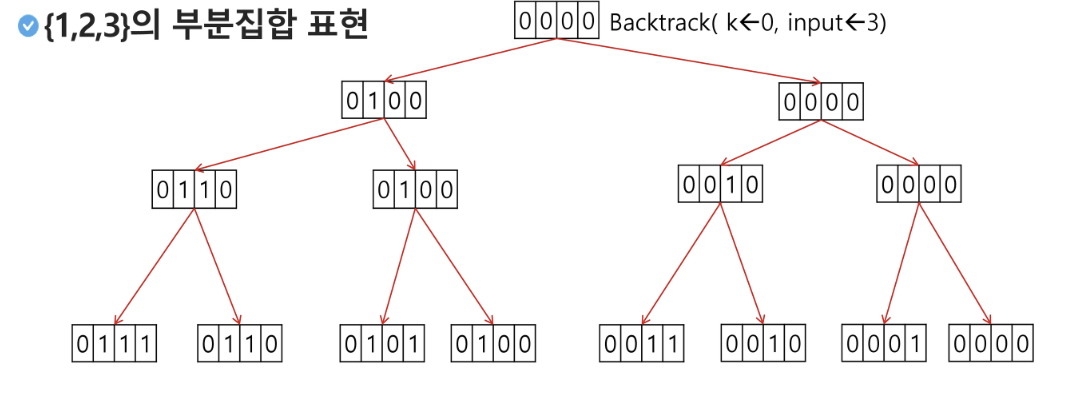
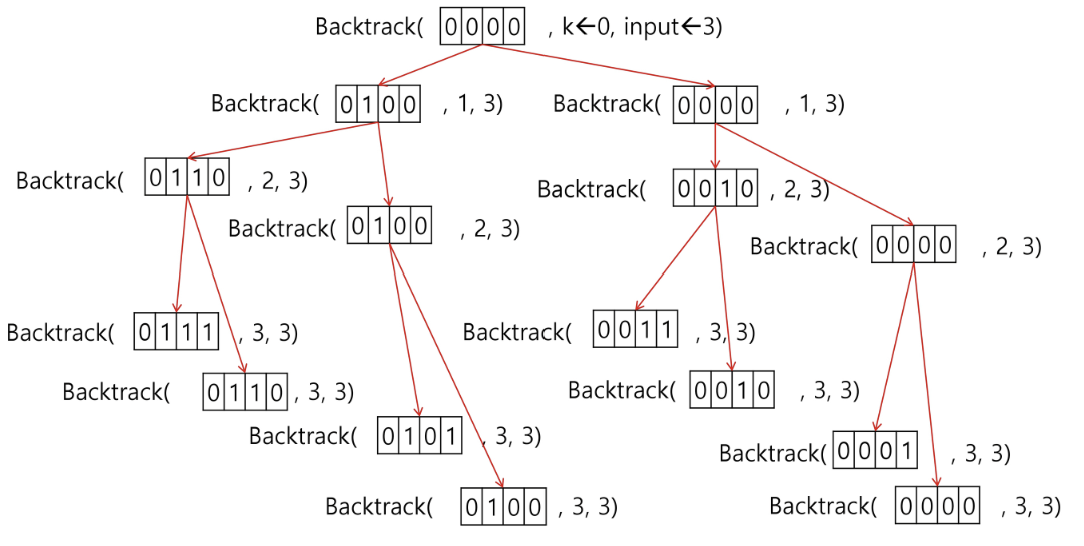
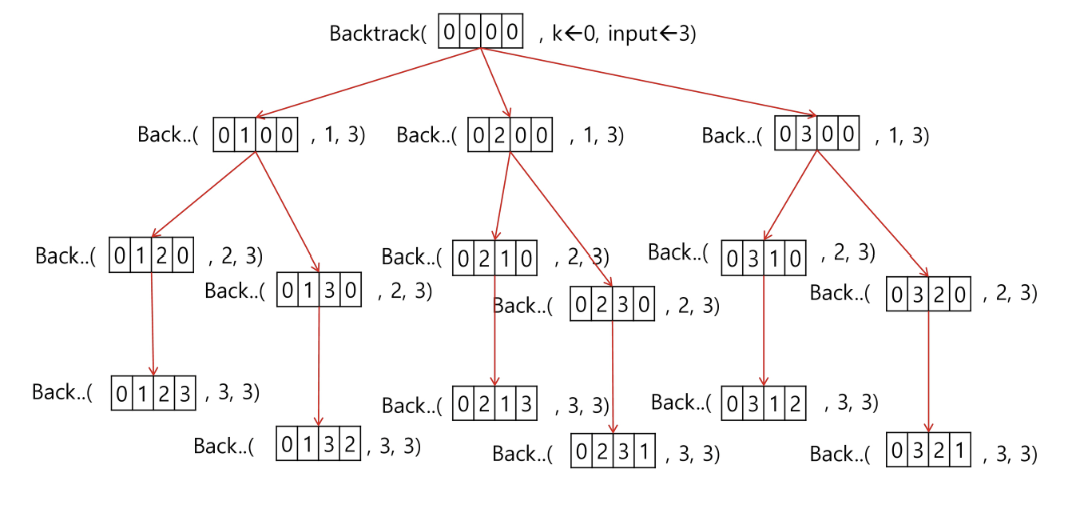
3. 부분집합 구하기
- 어떤 집합의 공집합과 자기자신을 포함한 모든 부분집합을 powerset이라고 하며 구하고자 하는 어떤 집합의 원소 개수가 n일 경우 부분집합의 개수는 2n개이다.
- 백트래킹 기법으로 powerset을 구해보자.
- 앞에서 설명한 일반적인 백트래킹 접근 방법을 이용한다.
- n개의 원소가 들어있는 집합의 2n개의 부분집합을 만들 때는, true 또는 false값을 가지는 항목들로 구성된 n개의 배열을 만드는 방법을 이용합니다.
- 여기서 배열의 i번째 항목은 i번째의 원소가 부분집합의 값인지 아닌지를 나타내는 값입니다.







'알고리즘' 카테고리의 다른 글
| 스택 - 분할정복 알고리즘 (0) | 2024.06.06 |
|---|---|
| 스택 - 부분집합 / 순열 (0) | 2024.06.05 |
| 스택 - 계산기2 (0) | 2024.06.03 |
| 스택 - 계산기1 (0) | 2024.06.02 |
| 스택 - DFS(깊이우선탐색) (0) | 2024.06.01 |





